
愚者小路
今日の400字は相関係数のリスク低減効果について。
経済全体がグローバル化してきた影響で代表的資産クラスの相関係数はだんだん上昇してきています。
もちろん相関係数1.0でない限りは分散効果は大なり小なりあるのですが、その「大なり小なり」ってどの程度なのか改めて確認してみましょう。
相関係数0.7以上だとリスクは1割も低減しない
図・表・引用文・動画・ソースコード・改行コード・スペース・事後補足は字数に含めないであげてください。

全く同じリスクを持つ資産ABを半々で併せ持つケースを想定する。
両者の相関係数が1~-1まで変化するとトータルのリスクがどれだけ変動するか計算してみよう。
計算式は下記の通り。文字で書くとクドいが、2資産系ならまだ書ける範囲だ。

| 相関係数 | トータルリスク |
|---|---|
| 1.00 | 20.00% |
| 0.90 | 19.49% |
| 0.80 | 18.97% |
| 0.70 | 18.44% |
| 0.60 | 17.89% |
| 0.50 | 17.32% |
| 0.40 | 16.73% |
| 0.30 | 16.12% |
| 0.20 | 15.49% |
| 0.10 | 14.83% |
| 0.00 | 14.14% |
| -0.10 | 13.42% |
| -0.20 | 12.65% |
| -0.30 | 11.83% |
| -0.40 | 10.95% |
| -0.50 | 10.00% |
| -0.60 | 8.94% |
| -0.70 | 7.75% |
| -0.80 | 6.32% |
| -0.90 | 4.47% |
| -1.00 | 0.00% |
一応-1まで書いたが、現実的な相関係数はあっても-0.3ぐらいまでだろう。
表を見ると相関係数0.6でようやくトータルリスクが1割程度低減できる。
暴落と呼ばれるような-2標準偏差の下落だと4%ほどダメージを軽減できる計算だ。
参考までに2021年までの各アセットクラス相関係数を示す。
別記事で集計した時のものだ。
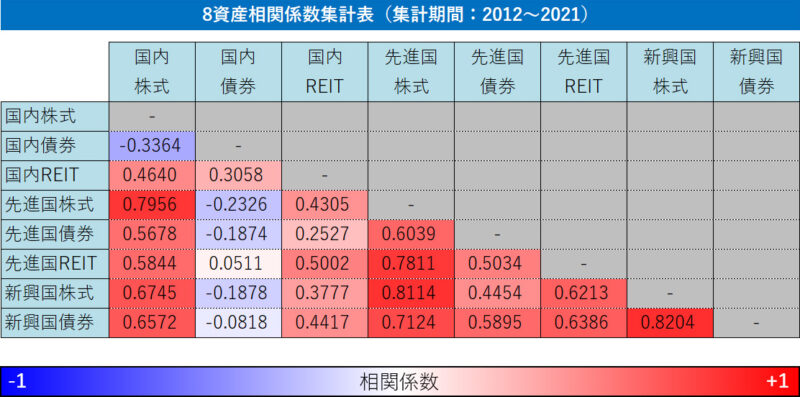
特に株式系の相関係数は非常に高くなっていて、分散効果が限定的なケースが目立つ。
「この程度でも分散効果はあるのだから国際分散続けよう」
「この程度なら分散効果が望めないのだから米国株集中で良いだろう」
覚悟さえあれば、どちらの結論に至ってもあながち間違いではないように思う。

【次回予告】さーて、次回の愚者小路さんは

愚者小路
愚者小路です。
Yahoo知恵袋には「このプランでFIREできますか?」という質問が案外多いです。
FIRE願望を持つ30歳派遣社員さんのFIREプランは詳細詰めてる一方で前提が激ヤバなのでした。

ありがとうございます。
次回もまた見てくださいね。
次回のタイトル/内容は予告なく変更する場合があります。ご了承ください。
YouTube「愚者小路の投信クエスト」も配信中。
こちらランキング参加中です。
応援していただくとより多くの方にご覧いただけるし、投稿モチベーションも上がります。
応援していただくとより多くの方にご覧いただけるし、投稿モチベーションも上がります。
↑いつもランキング向上にご協力ありがとうございます!
この記事を読んだ人はこんな記事も読んでいます
・・・なんて機能はないけれど、本件と関連が深い記事です。
もう1ページ、いかがですか?



















コメント